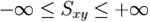Latest Entries »
DISTRIBUCIONES DE PROBABILIDAD DISCRETAS
DISTRIBUCIÓN DE PROBABILIDAD CONTINUA
Un número aleatorio es aquel obtenido al azar, es decir, que todo número tenga la misma probabilidad de ser elegido y que la elección de uno no dependa de la elección del otro. El ejemplo clásico más utilizado para generarlos es el lanzamiento repetitivo de una moneda o dado ideal no trucado.
FUENTE
http://www.estadisticaparatodos.es/taller/aleatorios/aleatorios.html
Los números aleatorios son números que están entre (0 & 1) pero pueden incluirse en el cero y el uno. El mecanismo para números aleatorios es el pseudoaleatorio. Los números pseudoaleatorios, están entre 0 y 1, pero nunca serán 0 y nunca serán uno (se toma como algo imaginario). Estos números son utilizados por los mecanismos de generación. Entre los primeros mecanismos de generación de números aleatorios, se encuentran la ruleta, las cajas eléctricas, entre otros.
FUENTE
GONZALEZ CONDE, Medardo. Clase de Simulación de procesos empresarial. 28 de Febrero 2011.
HISTORIA
Aproximadamente alrededor del año 3500 a.C., los juegos de azar eran practicados con objetos de hueso, los cuales podrían ser considerados como los precursores de los dados, estos fueron ampliamente desarrollados en Egipto y otros lugares. En el siglo XVII, un noble francés, Antoine Gombauld (1607-1684), puso en tela de juicio el fundamento matemático del éxito y del fracaso en las mesas de juego y por esto le formuló la siguiente pregunta al matemático francés Blaise Pascal (1623-1662): ¿cuales son las probabilidades de que salgan dos de seises por lo menos una vez en veinticuatro lanzamientos de una par de dados?, pascal resolvió el problema, pues la teoría de probabilidad empezaba a interesarle tanto como a gombauld. Ambos compartieron sus ideas con el famoso matemático Pierre de Fermat (1601-1665), y las cartas escritas por los tres constituyen la primera revista académica dedicada a la probabilidad. Algunos de los problemas que ellos resolvieron habían permanecido sin solución durante unos 300 años. Sin embargo, ciertas probabilidades numéricas para ciertas combinaciones de dados ya habían sido calculadas por Giordamo Cardano (1501-1576) y por Galileo Galilei (1564-1642).
Más tarde, Jacob Bernoulli (1654-1705), Abraham de Moivre (1667-1754), el reverendo Thomas Bayes (1702-1761) y Joseph LaGrange (1736-1813) inventaron formulas y técnicas de probabilidad. En el siglo XIX, Pierre Simón, Marques Delaplace (1749-1827), unifico esas primeras ideas y formulo la primera teoría general de la probabilidad, la cual fue aplicada inicialmente con buenos resultados a los juegos de azar; con el tiempo también se aplico en la búsqueda de soluciones analíticas a problemas de naturaleza no deterministica. La teoría de la probabilidad ha sido constantemente desarrollada desde el siglo XVII y ampliamente aplicada en diversos campos de estudio. Hoy es una herramienta importante en la mayoría de las áreas de ingeniería, ciencias y administración, y se constituye en la base para el estudio de fenómenos o procesos aleatorios mediante el método de Montecarlo, que es el estudio de las leyes de azar.
En cuanto a los números aleatorios, se puede afirmar que la historia formal comenzó en la década de los cuarenta con el nacimiento del método llamado simulación de Montecarlo, y Von Neumann, Metrópolis, Ulam y Lehmer son considerados y nombrados como los pioneros en este campo. John Von Neumann aparentemente conjeturo el potencial de los computadores para tratar problemas estocásticos en 1945 cuando escribió: “este (el computador) ciertamente abrirá un nuevo enfoque para la estadística matemática, el enfoque para el cálculo de experimentos”. Durante los cuarenta, la simulación de procesos estocásticos permaneció restringida al proyecto secreto del departamento de defensa de estados unidos. La publicación de The Monte Carlo Method por N. metrópolis y Stanislaw M. Ulam en 1949 denota el inicio de la historia oficial del método. Dos años más tarde, D.H.Lehmer propuso el generador lineal de congruencia, el cual, con pequeñas modificaciones propuestas por Thomson y Rotenberg, ha llegado a convertirse en el método para la generación de números aleatorios mas ampliamente usado en la actualidad. Aunque originalmente el método de Montecarlo fue implementado por John Neumann y Stanislaw Ulam, utilizando ruletas y dados en los problemas de difusión de los neutrones, en realidad su auge y crecimiento uso se debe a que hoy se emplean números aleatorios generados por computador.
Antes de la aparición de las computadoras, los números aleatorios eran generados por dispositivos físicos. En 1939, Kendall y Babington-Smith publicaron 100.000 dígitos aleatorios obtenidos con un disco giratorio iluminado con una lámpara relámpago. En 1955, la rand Corporation publico un millón de dígitos producidos controlando una fuente de pulsos de frecuencia aleatoria (mecanismo electrónico); estos se encuentran disponibles en cintas magnéticas de la rand.
FUENTE
PDF: Números aleatorios “historia, teoría y aplicaciones”. Alfonso Manuel Mancilla Herrera. Ingeniería & desarrollo. Universidad del norte. 10 de octubre del 2000.
http://manglar.uninorte.edu.co/bitstream/10584/1559/1/numeros_aleatorios.pdf
Generación de números aleatorios con método congruencial
Los generadores de números aleatorios que más se usan son los generadores congruenciales lineales (LCG) ideados por Lehmer. El propósito de un LCG es generar un valor aleatorio a partir de otro anterior. Aquí se muestran el métodos congruenciales mixto.
Congruencial Mixto
La fórmula (o relación de recurrencia) es sencilla:
Donde:
- X0 es la semilla
- a el multiplicador
- c la constante aditiva y
- m el módulo
A tener en cuenta: Los valores a, X0 y c tienen que ser mayores que cero. Y la variable m tiene que ser mayor que las tres anteriores. Para entrar en acción vamos a darle valores arbitrarios a cada uno de estos parámetros y estudiar qué reacción tienen en la relación de recurrencia. Supongamos que a = 5, c = 7, X0 = 7 y m = 8. Entonces los resultados son:
| n | Xn | Xn + 1 |
| 0 | 7 | 2 |
| 1 | 2 | 1 |
| 2 | 1 | 4 |
| 3 | 4 | 3 |
| 4 | 3 | 6 |
| 5 | 6 | 5 |
| 6 | 5 | 0 |
| 7 | 0 | 7 |
| … | … | … |
Nótese que después de 8 pasadas el valor inicial de X se repite. Decimos entonces que el periodo del generadores 8… igualito al valor del módulo… Eso no siempre es así. Veamos un caso donde el periodo es menor a m. El valor de los parámetros es a = c = X0 = 4 y m = 6. Ahora lo resultados son:
| n | Xn | Xn + 1 |
| 0 | 4 | 6 |
| 1 | 6 | 0 |
| 2 | 0 | 4 |
| … | … | … |
Fuente
http://314159bits.wordpress.com/2010/09/19/generar-numeros-aleatorios-con-metodo-congruenciales/
PRUEBA DE KOLMOGOROV-SMIRNOV
Sirve para verificar o negar la hipótesis que un conjunto de observaciones provienen de una distribución. La estadística D que se utiliza en esta prueba es una medida de la diferencia máxima observada entre la distribución empírica y la teórica supuesta. D es una variable aleatoria. Se utiliza esta prueba para verificar o negar que un conjunto de números pseudoaleatorios tienen una distribución uniforme en el intervalo cerrado [0,1].
Fuente bibliográfica
“Introducción a la Simulación”. Disponible en < http://wwwdi.ujaen.es/asignaturas/computacionestadistica/pdfs/tema1.pdf>.
Procedimiento:
1. Formular la hipótesis nula, H0. Teniendo en cuenta que los números que se van a generar provienen de una distribución uniforme.
2. Se selecciona una muestra de tamaño n de números pseudoaleatorios n.
3. Se hallan los parámetros de acuerdo a la distribución que se esté utilizando y demás datos que sirvan de base para la realización de la prueba. Ej.: para el caso de una distribución normal se deben hallar los parámetros respectivos (Media, desviación estándar) y otros datos de utilidad.
4. Se debe calcular la función de distribución acumulada para después hallar las frecuencias respectivas.
5. Antes de poder hallar el estadístico de prueba se debe hallar la frecuencia observada y la frecuencia relativa de cada uno de los intervalos establecidos de acuerdo al rango.
6. Se aplica la ecuación D= Frecuencia observada relativa-Frecuencia esperada relativa para hallar la discrepancia de las mismas o error estadístico.
7. Posteriormente, se halla el estimador Smirnov-Kolmogorov que es: Valor máximo entre todos los valores hallados para cada intervalo. En Excel sería =Máx. [Frecuencia observada relativa-Frecuencia esperada relativa].
8. Se hallan también los grados de libertad de acuerdo a la distribución estadística utilizada. A su vez se establece un nivel de significancia de acuerdo al planteamiento.
9. Con base a lo anterior se consulta la tabla de límites de aceptación para la prueba de Kolmogorov-Smirnov para un tamaño de muestra n y un determinado nivel de riesgo alfa, Si el estimador de la prueba es menor al valor buscado en la tabla se acepta H0 o hipótesis nula, en caso contrario se rechaza.
Fuente: MILLER, Irwin. FREUND, John E. Probabilidad y estadística para ingenieros. Editorial Reverté, S.A. Pág 207-208.
Prueba de medios: Consiste en verificar que los números generados tengan una media estadísticamente igual a ½, de este modo la hipótesis planteada es:
H0= Hipótesis nula: μ= ½
H1 = Hipótesis alternativa: μ Diferente de ½.
Pasos a seguir en esta prueba:
1. Calcular la media de los n números generados:
2. Calcular los límites superior e inferior de aceptación
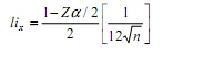
Si el valor de la media se encuentra entre el límite inferior y el límite superior se acepta entonces que los números aleatorios tienen una media estadísticamente igual a ½ con un nivel de aceptación de 1- α.
Prueba de varianza: Consiste en verificar si los números aleatorios generados tienen una varianza de 0.083, de tal forma que la hipótesis queda expresada como:
El procedimiento a seguir para el uso de este tipo de prueba, es el siguiente:
1. Calcular la variancia de los n números generados V(x).
2. Calcular los límites superior e inferior de aceptación:
Si V(x) se encuentra entre los valores de los límites anteriores, entonces se acepta la hipótesis nula y los números aleatorios tienen una varianza estadísticamente igual a 1/12.
Prueba de poker: Las pruebas de independencia consisten en demostrar que los números generados son estadísticamente independientes entre sí, esto es, que no depende uno de otro. Hay varios métodos, entre los cuales están:
- La prueba de Poker.
- La prueba de corridas arriba y abajo.
- La prueba de corridas arriba debajo de la media.
- La prueba de la longitud de las corridas.
- La prueba de series
La prueba de poker plantea la siguiente hipótesis:
H0: ri ~ independiente
H1: ri ~ dependiente
El procedimiento a seguir en esta prueba, es el siguiente:
1. Calcular las probabilidades esperadas para un juego de poker con 5 cartas numeradas del 0 al 9 con reemplazos. Se tienen 7 eventos con las siguientes probabilidades:
Calcular la frecuencia esperada de cada uno de los eventos multiplicando la probabilidad de cada evento por la cantidad de números aleatorios generados.
Para cada número aleatorio generado verificar si es pachuca, 1 par, 2 pares, etc., tomando los primeros 5 dígitos a la derecha del punto decimal. Con estos resultados se genera una tabla de frecuencias observadas de cada uno de los eventos.
Calcular la estadística:
Si el valor de XI2 es menor o igual al estadístico de tablas XI2 con m-1 grados de libertad y una probabilidad de rechazo, entonces se acepta que estadísticamente los números son independientes.
Fuente bibliográfica
“Introducción a la Simulación”. Disponible en < http://wwwdi.ujaen.es/asignaturas/computacionestadistica/pdfs/tema1.pdf>.
PRUEBA DE CHI-CUADRADO
Se usa cuando se quiere probar la hipótesis de que unos datos muéstrales provienen de una determinada distribución.
La prueba chi2 se basa en la comparación entre la frecuencia observada en un intervalo de clase y la frecuencia esperada en dicho intervalo, calculada de acuerdo con la hipótesis nula formulada. Es decir, se quiere determinar si las frecuencias observadas en la muestra están lo suficientemente cerca de las frecuencias esperadas bajo la hipótesis nula.
Para esta prueba es necesario agrupar o distribuir las observaciones de la muestra en intervalos de clase, preferiblemente del mismo tamaño. El estadístico de prueba está definido como:
Donde: Oi = Total de valores que caen en el intervalo i.
Ei = Número esperado de valores en el intervalo i.
k = Número de intervalos de clase en que se distribuyen las observaciones.
Si los límites del intervalo de clase i están dados por Xi-1 y Xi, como lo ilustra la presente gráfica, el número esperado de observaciones para ese intervalo está dado por:
Ei =nPi
Donde Pi representa la probabilidad de que una observación quede en el intervalo i, de acuerdo con función de densidad que se esté analizando, y n es el número total de observaciones.
La probabilidad de que una observación caiga en el intervalo i está dada por:
Donde f0(x, θ) es la función de densidad de la variable aleatoria X, bajo la hipótesis nula.
Fuente bibliográfica
“Introducción a la Simulación”. Disponible en < http://wwwdi.ujaen.es/asignaturas/computacionestadistica/pdfs/tema1.pdf>.
PROCEDIMIENTO:
- Se debe identificar la variable de interés.
- Se identifica la hipótesis nula H0. Teniendo en cuenta de cuál distribución provienen los números que se van a generar.
- Se identifican los parámetros de acuerdo a la distribución que se esté utilizando para poder hallar así el número de intervalos que saldrán de acuerdo a la cantidad de números aleatorios generados.
- Posteriormente debe hacerse el cálculo de la frecuencia observada con base a los límites establecidos de cada intervalo.
- Es hallada la frecuencia relativa esperada acumulada y a su vez la frecuencia relativa esperada teniendo en cuenta el tipo de distribución que se esté usando para el problema planteado, datos base para el estadístico de prueba chi cuadrado. Ej.: en caso de que se este utilizando una distribución normal en el programa Excel, esta frecuencia relativa esperada sería igual a: =Distr.norm (Límite superior de intervalo, Media, Desviación, Verdadero)
- Por otra parte es calculada la frecuencia observada esperada que es igual: Frecuencia observada esperada = Frecuencia relativa esperada de cada intervalo * Total de frecuencia observada.
- Se calcula el estadístico de prueba el cual está dado por la siguiente fórmula:

8. Antes de saber si se rechaza o se acepta la hipótesis, se debe tener en cuenta el nivel de significancia que se escoja para el problema.
9Entonces, con base al nivel de significancia y a los grados de libertad se puede calcular el valor que permitirá saber si se acepta o no la prueba.
10. Se compara el valor hallado en la tabla de chi2 con el estimador hallado, si este último es menor al valor de la tabla, entonces se acepta la hipótesis, en caso contrario se rechaza
11. Con base a los resultados se establecen las conclusiones pertinentes de la prueba chi2.
Fuente Bibliografica
SERRANO CAMPOS, Eduardo. Simulación de sistemas. 26 de septiembre de 2009.
Prueba de poker: Las pruebas de independencia consisten en demostrar que los números generados son estadísticamente independientes entre sí, esto es, que no depende uno de otro. Hay varios métodos, entre los cuales están:
La prueba de Poker.
La prueba de corridas arriba y abajo.
La prueba de corridas arriba debajo de la media.
La prueba de la longitud de las corridas.
La prueba de series
La prueba de poker plantea la siguiente hipótesis:
H0: ri ~ independiente
H1: ri ~ dependiente
El procedimiento a seguir en esta prueba, es el siguiente:
1. Calcular las probabilidades esperadas para un juego de poker con 5 cartas numeradas del 0 al 9 con reemplazos. Se tienen 7 eventos con las siguientes probabilidades:
Calcular la frecuencia esperada de cada uno de los eventos multiplicando la probabilidad de cada evento por la cantidad de números aleatorios generados.
Para cada número aleatorio generado verificar si es pachuca, 1 par, 2 pares, etc., tomando los primeros 5 dígitos a la derecha del punto decimal. Con estos resultados se genera una tabla de frecuencias observadas de cada uno de los eventos.
Calcular la estadística:
Si el valor de XI2 es menor o igual al estadístico de tablas XI2 con m-1 grados de libertad y una probabilidad de rechazo, entonces se acepta que estadísticamente los números son independientes.
Fuente bibliográfica
“Introducción a la Simulación”. Disponible en < http://wwwdi.ujaen.es/asignaturas/computacionestadistica/pdfs/tema1.pdf>.
PRUEBA DE ANDERSON DARLING
Fue conocida en 1954, prueba tiene como propósito corroborar si una muestra de variables aleatorias proviene de una población con una distribución de probabilidad específica. Trata de una modificación de la prueba de kolmogorov-smirnov, aunque tiene la virtud de detectar las discrepancias en los extremos de las distribuciones. La principal desventaja que es necesario calcular los valores críticos para cada distribución. Esta es muy sensible en los extremos de la distribución, por lo que debe ser usada con mucho cuidado en distribuciones con límite inferior acotado, y no es confiable para distribuciones de tipo discreto.
PROCEDIMIENTOS:
- Obtener n datos de la variable aleatoria a analizar.
- Calcular la media y la varianza de los datos.
- Organizar los datos en forma ascendente: Yi i=1,2….,n.
- Ordenar los datos en forma descendente Yn+1-i i = 1,2….,n.
- Establecer explícitamente la hipótesis nula, proponiendo una distribución de probabilidad.
- Calcular la probabilidad esperada acumulada para cada número Yi, PEA(Yi), y la probabilidad esperada acumulada para cada número, PEA(Yn+1-i), a partir de la función de probabilidad propuesta.
- Calcular el estadístico de prueba:

8. Ajustar el estadístico de prueba de acuerdo con la distribución de probabilidad propuesta}
9. Definir el nivel de significancia de la prueba α, y determinar su valor crítico.
10. Comparar el estadístico de prueba con el valor crítico. Si el estadístico de prueba es menor el valor crítico no se puede rechazar la hipótesis nula.
Fuente Bibliográfica
GARCÍA DUNNA, Eduardo. GARCÍA REYES, Heriberto. CÁRDENAS BARRÓN, Leopoldo Eduardo. Simulación y análisis de sistemas con promodel. Primera edición. Editorial Pearson educación, México 2006. Pág 62-64.
Durante los últimos años los avances han posibilitado la utilización de la simulación en la investigación. Uno de los procedimientos de simulación más utilizados es el método de Monte Carlo. Este método se aplica en la resolución de problemas matemáticos que resultan técnicamente inmanejables o cuya solución requiere un alto costo en términos de tiempo de trabajo, mediante la simulación de procesos aleatorios. Una limitación de este procedimiento es que las conclusiones, por ser resultado de un procedimiento experimental, son relativas a los procesos utilizados en la simulación.
Bajo el nombre de “Método de Monte Carlo” o “Simulación Monte Carlo” se agrupan una serie de procedimientos que analizan distribuciones de variables aleatorias usando simulación de números aleatorios. El Método de Monte Carlo da solución a una gran variedad de problemas matemáticos haciendo experimentos con muestreos estadísticos en una computadora. El método es aplicable a cualquier tipo de problema, ya sea estocástico o determinístico.
Generalmente en estadística los modelos aleatorios se usan para simular fenómenos que poseen algún componente aleatorio. Pero en el método de Monte Carlo, por otro lado, el objeto de la investigación es el objeto en sí mismo, un suceso aleatorio o pseudo-aleatorio se usa para estudiar el modelo.
La simulación de Monte Carlo fue creada para resolver integrales que no se pueden resolver por métodos analíticos, para resolver estas integrales se usaron números aleatorios. Posteriormente se utilizó para cualquier esquema que emplee números aleatorios, usando variables aleatorias con distribuciones de probabilidad conocidas, el cual es usado para resolver ciertos problemas estocásticos y determinísticos, donde el tiempo no juega un papel importante.
Durante la Guerra Fría se intensificó el uso de la simulación para resolver problemas de interés militar; trayectorias y dinámicas de satélites artificiales, guiar mísiles, etc. Muchos de estos problemas exigen la resolución de sistemas de ecuaciones diferenciales no lineales. Para abordar estos problemas se utilizaron ordenadores analógicos que usaban elementos electrónicos para resolver las operaciones matemáticas: integración, suma, multiplicación, generación de funciones, etc.
A partir de la década de los 60 empiezan a aparecer en el mercado programas de simulación de sistemas de acontecimientos discretos que poco a poco se empezaron a utilizar para resolver problemas de ámbito civil. Los más destacables fueron el GPSS de IBM (General Purpose System Simulator) y el SIMSCRIPT. Los modelos de acontecimientos discretos son muy utilizados en la actualidad para estudiar problemas de fabricación de procesos, logística, transporte, comunicaciones y servicios. Estos problemas se caracterizan por centrar su interés en los cambios que hay en el sistema como consecuencia de los acontecimientos y en su capacidad para modelar los aspectos aleatorios del sistema. Este simulador se utilizó para analizar el diseño de la terminal(Barcelona) en lo que respecta a los distintos espacios, el movimiento de las personas en situaciones normales y el análisis del plan de evacuación.
La revolución que se produjo en la informática a partir de los años 80, tiene un impacto importante en la simulación por ordenador. El uso de simuladores se generaliza en prácticamente todos los ámbitos de la ciencia y la ingeniería, por ejemplo:
- Predicción del tiempo: el primer modelo numérico de predicción del tiempo que dio resultados positivos fue desarrollado por J. G. Charney, R. Fjörtoft y J. von Neumann con el ordenador «ENIAC» (Electronic Numerical Integrator and Computer). Desde entonces, y especialmente en las últimas dos décadas, se han popularizado estos simuladores para la predicción a corto y largo plazo del tiempo.
- Entrenamiento de pilotos: la necesidad de entrenar los pilotos surge ya en los inicios de la aviación. A falta de ordenadores y programas informáticos de simulación, los primeros pilotos se entrenaban con primitivos simuladores físicos. Actualmente, todos los pilotos están obligados a entrenar-se periódicamente en sofisticados simuladores para estar preparados para resolver cualquier problema que pueda aparecer en el vuelo.
Finalmente, en los últimos años, el uso de la simulación se ha ampliado al sector del ocio y ha entrado en el ámbito familiar con productos de software sofisticado, que utilizan todos los recursos del ordenador: gráficos potentes, bases de datos, computación intensiva, etc. Algunos de los simuladores más populares son MS Flight Simulator, NASCAR Racing, SimCity, Civilization, RollerCoaster Tycoon, y The Sims.
La simulación de procesos a lo largo del tiempo ha permitido resolver cuestiones complejas para las cuales los métodos cuantitativos no son eficaces o no pueden aplicarse. Robert Shannon lo define como “el proceso de diseñar y desarrollar un modelo de sistema o proceso, y conducir experimentos con este modelo con el propósito de entender el comportamiento del sistema o evaluar estrategias con las cuales se puede operar sobre él”1; es por esto que se ha diseñado este espacio o herramiento con el fin de tener acceso a conocimientos ya estudiados para desarrollar la creatividad y construir conocimiento.
Dentro de esta herramienta se encontrara diversidad de concepto tomando como base principal la SIMULACION EMPRESARIAL DE PROCESOS, se expondrán diferentes manera para simular, modelos como también se abrirá paso a exponer lo referente a la experimentación con un modelo que conlleva normalmente a la necesidad de generar datos y/o investigar parámetros a efectos de analizar el comportamiento global del mismo o la sensibilidad a los distintos parámetros; teniendo en cuenta sus respectivas fuentes bibliográficas.
BIBLIOGRAFIA
1http://www.casp.ubiobio.cl/index.php?option=com_content&view=article&id=50&Itemid=56
http://www.fib.upc.edu/retro-informatica/avui/simulacio.html
Las medidas de dispersión, también llamadas medidas de variación, muestran la variabilidad de una distribución, indicando por medio de un número, si las diferentes puntuaciones de una variable están muy alejadas de la media. Cuanto mayor sea ese valor, mayor será la variabilidad, cuanto menor sea, más homogénea será a la media
Para calcular la variabilidad que una distribución tiene respecto de su media, se calcula la media de las desviaciones de las puntuaciones respecto a la media aritmética. Pero la suma de las desviaciones es siempre cero, así que se adoptaran dos clases de estrategias para salvar este problema. Una es tomando las desviaciones en valor absoluto (Desviación media) y otra es tomando las desviaciones al cuadrado (Varianza).
Varianza, es una medida de desorden de los datos. Medida de error. Suele ser representada con la letra griega σ o una V en mayúscula.
Propiedades
- La varianza es siempre positiva o 0:
- Si a los datos de la distribución le suman una cantidad constante la varianza no se modifica.
Yi
-
Si a los datos de la distribución se les multiplicamos una constante, la varianza queda multiplicada por el cuadrado de esa constante.
-
Propiedad distributiva: V(X + Y) = V(X) + V(Y)
Rango o recorrido estadístico, es una medida primaria; es la diferencia entre el valor mínimo y el valor máximo en un grupo de números aleatorios. Se le suele simbolizar con R.
Requisitos del rango
- Ordenamos los números según su tamaño.
- Restamos el valor mínimo del valor máximo.
Ejemplo
Para una muestra (8,7,6,9,4,5), el dato menor es 4 y el dato mayor es 9 (Valor unitario inmediatamente posterior al dato mayor menos el dato menor). Sus valores se encuentran en un rango de:
Rango = 5
Medio rango es la media del menor y mayor valor, o la mitad del camino entre el dato de menor valor y el dato de mayor valor. En consecuencia el medio rango es:
Ejemplo
Para una muestra de valores (3, 3, 5, 6, 8), el dato de menor valor Min= 3 y el dato de mayor valor Max= 8. El medio rango resolviéndolo mediante la correspondiente fórmula sería:
Desviación típica, La varianza a veces no se interpreta claramente, ya que se mide en unidades cuadráticas. Para evitar ese problema se define otra medida de dispersión, que es la desviación típica, se halla como la raíz cuadrada positiva de la varianza. La desviación típica informa sobre la dispersión de los datos respecto al valor de la media; cuanto mayor sea su valor, más dispersos estarán los datos. Esta medida viene representada en la mayoría de los casos por S, dado que es su inicial de su nominación en inglés.
Desviación típica muestral
Desviación típica poblacional
Covarianza, entre dos variables es un estadístico resumen indicador de si las puntuaciones están relacionadas entre sí. La formulación clásica, se simboliza por la letra griega sigma (σ) cuando ha sido calculada en la población. Si se obtiene sobre una muestra, se designa por la letra «sxy«.
Formula:
Este tipo de estadístico puede utilizarse para medir el grado de relación de dos variables si ambas utilizan una escala de medida a nivel de intervalo/razón (variables cuantitativas).
La expresión se resuelve promediando el producto de las puntuaciones diferenciales por su tamaño muestral (n pares de puntuaciones, n-1 en su forma insesgada). Este estadístico, refleja la relación lineal que existe entre dos variables. El resultado numérico fluctua entre los rangos de +infinito a -infinito. Al no tener unos límites establecidos no puede determinarse el grado de relación lineal que existe entre las dos variables, solo es posible ver la tendencia.
Coeficiente de Correlación de Pearson r, permite saber si el ajuste de la nube de puntos a la recta de regresión obtenida es satisfactorio. Se define como el cociente entre la covarianza y el producto de las desviaciones típicas (raíz cuadrada de las varianzas).
Teniendo en cuenta el valor de la covarianza y las varianzas, se puede evaluar mediante cualquiera de las dos expresiones siguientes:
Propiedades
- El coeficiente de correlación, r, presenta valores entre –1 y +1.
- Cuando r es próximo a 0, no hay correlación lineal entre las variables. La nube de puntos está muy dispersa o bien no forma una línea recta. No se puede trazar una recta de regresión.
- Cuando r es cercano a +1, hay una buena correlación positiva entre las variables según un modelo lineal y la recta de regresión que se determine tendrá pendiente positiva, será creciente.
- Cuando r es cercano a -1, hay una buena correlación negativa entre las variables según un modelo lineal y la recta de regresión que se determine tendrá pendiente negativa: es decreciente.
Las medidas de tendencia central corresponden a valores que generalmente se ubican en la parte central de un conjunto de datos. (Ellas permiten analizar los datos en torno a un valor central). Entre éstas están la media aritmética, la moda y la mediana.
La media aritmética es el numero que representa un grupo de números, interpretando como si todos los valores del grupo tuvieron el mismo valor.
| ( X )=SIMBOLO |
| X | = | suma de todos los valores | = | x1 + x2 + x3 + x4 + …… |
| número total de datos | n |
Ejemplo:
En matemáticas, un alumno tiene las siguientes notas: 4, 7, 7, 2, 5, 3
n = 6 (número total de datos)
| X | = | 4 + 7 + 7 + 2 + 5 + 3 | = | 28 | = | 4,8 |
| 6 | 6 |
La media aritmética de las notas de esa asignatura es 4,8. Este número representa el promedio.
La moda(Mo), es el valor que más se repite de un conjunto de datos, es decir; que cuando algo se repite se vuelve clásico; indica cual dato tiene la mayor frecuencia en un conjunto de datos.
Ejemplo:
Determinar la moda en el siguiente conjunto de datos que corresponden a las edades de niñas de un Jardín Infantil.
5, 7, 3, 3, 7, 8, 3, 5, 9, 5, 3, 4, 3
La edad que más se repite es 3, por lo tanto, la Moda es 3 (Mo = 3)
La mediana. Es el número de la mitad en un conjunto de números, la Mediana corresponde al valor que deja igual número de valores antes y después de él en un conjunto de datos agrupados.
Según el número de valores que se tengan se pueden presentar dos casos:
1) Si el número de valores es impar, la Mediana corresponderá al valor central de dicho conjunto de datos.
2) Si el número de valores es par, la Mediana corresponderá al promedio de los dos valores centrales (los valores centrales se suman y se dividen por 2).
Ejemplo 1:
Se tienen los siguientes datos: 5, 4, 8, 10, 9, 1, 2
Al ordenarlos en forma creciente, es decir de menor a mayor, se tiene:
1, 2, 4, 5 , 8, 9, 10
El 5 corresponde a la Med, porque es el valor central en este conjunto de datos impares.
Ejemplo 2:
El siguiente conjunto de datos está ordenado en forma decreciente, de mayor a menor, y corresponde a un conjunto de valores pares, por lo tanto, la Med será el promedio de los valores centrales.
21, 19, 18, 15, 13, 11 ,10, 9, 5, 3
| Med | = | 13 + 11 | = | 24 | = | 12 |
| 2 | 2 |
Fuente bibliográfica
“Introducción a la Simulación”. Disponible en < http://wwwdi.ujaen.es/asignaturas/computacionestadistica/pdfs/tema1.pdf>.
Un modelo es una representación de un objeto de interés. No obstante que el objeto sea único, el número de representaciones es por lo general muy grande, de modo que el número de modelos de un sistema del mundo real lo es también. Puesto que para un sistema del mundo real habrá tantas representaciones como concepciones de la realidad se tengan, el número de modelos es por lo general infinito. El hecho de que se tenga más de un modelo de simulación para un sistema real, no es de preocupación, encontrar un modelo de simulación casi siempre es fácil, mientras que encontrar un modelo analítico con frecuencia es una tarea ardúa, independientemente que, para muchos problemas, un modelo analítico, simplemente no existe.
Fuente Bibliográfica
http://cadit.anahuac.mx/~sac/download/35/MAD524/p/introsim.htm
1. MODELOS SIMBÓLICOS: Son más específicos que los modelos verbales. Ellos representan un puente útil en el proceso de simbolizar un modelo verbal. Estos aíslan las variables y representan la realidad a través de símbolos, los que tienen generalmente un carácter matemático o lógico. Estos pueden clasificarse en:
1.1 Modelos matemáticos: Son más rigurosos; se valen de variables cuantitativas, como fórmulas para representar las partes de un proceso o un sistema. También son los más abstractos y a la vez, los más fáciles de usar debido a que todas las relaciones están expresadas con precisión, reduciendo así la posibilidad de malas interpretaciones por los usuarios del modelo. Estos modelos a su vez se clasifican en:
1.1.1 Modelos cuantitativos: es aquel cuyos principales símbolos representan números. Son los más comunes y útiles en los negocios.
1.1.2 Modelos cualitativos: aquel modelo cuyos símbolos representan en su mayoría a Cualidades no numéricas. Una fuente importante es la teoría de conjuntos.
1.1.3 Modelo Probabilístico: aquellos basados en la estadística y probabilidades (donde se incorpora las incertidumbres que por lo general acompañan nuestras observaciones de eventos reales). Este modelo se clasifica en discreto y continuo.
- Modelo probabilístico continuos: Representan sistemas cuyos cambios de estado son graduales. Las variables intervinientes son continuas.
- Modelo probabilístico discreto: Representan sistemas cuyos cambios de estado son de a saltos. Las variables varían en forma discontinua.
- Modelo estocástico: Representan sistemas donde los hechos suceden al azar, lo cual no es repetitivo. No se puede asegurar cuáles acciones ocurren en un determinado instante. Se conoce la probabilidad de ocurrencia y su distribución probabilística. (Por ejemplo, llega una persona cada 20 ± 10 segundos, con una distribución x probable dentro del intervalo).
1.1.4 Modelo Deterministico: corresponde a aquel modelo cuantitativo que no contiene consideraciones probabilísticas.
1.1.5 Modelo Descriptivo: cuando el modelo simplemente describe una situación del mundo real en términos matemáticos, descripción que puede emplearse para exponer una situación con mayor claridad, para indicar como pueden reajustarse o aún para determinar los valores de ciertos aspectos de la situación.
1.1.6 Modelo Optimizador: corresponde al modelo ideado para seleccionar entre varias alternativas, de acuerdo a determinados criterios, la más óptima.
1.1.7 Modelo estático: Utilizados para representar sistemas cuyo estado es invariable a través del tiempo. El modelo estático puede ser:
- Modelo numérico: Se tiene el comportamiento numérico de las variables intervinientes. No se obtiene ninguna solución analítica.
- Modelo analítico: La realidad se representa por fórmulas matemáticas.
1.1.8 Modelo dinámico: Utilizados para representar sistemas cuyo estado varía con el tiempo. Estos pueden ser:
- Modelo numérico: Se tiene el comportamiento numérico de las variables intervinientes. No se obtiene ninguna solución analítica.
- Modelo analítico: La realidad se representa por fórmulas matemáticas. Estudiar el sistema consiste en operar con esas fórmulas matemáticas (resolución de ecuaciones).
1.2. Modelos verbales: Explicación con palabras de lo fundamental de una realidad.
2. MODELOS MENTALES: Son un conjunto de conceptos que conforman la estructura mental a través de la cual percibimos el mundo exterior y las experiencias personales.
Este conjunto de conceptos es el producto de la enseñanza, los patrones culturales, la experiencia y el entrenamiento.
3. MODELOS FÍSICOS: Representan la entidad estudiada en cuanto a su apariencia y, hasta cierto punto, en cuanto a sus funciones. Las actividades del sistema se reflejan en las leyes físicas que subyacen el modelo. Estos se clasifican en:
3.1.1 Modelo icónico: Tienen aspecto de realidad pero no se comportan efectivamente en la forma real.
3.1.2 Modelo analógico: Exhiben el comportamiento real de la entidad estudiada pero no tiene el mismo aspecto.
3.1.3 Modelo digital: El objeto se codifica en cifras organizadas en estructura de datos. Las relaciones de correspondencia son matemáticas, estadísticas o geométricas.
3.1.4 Modelo estático: Corresponden a los modelos a escala así como los modelos icónicos.
3.1.5 Modelo dinámico: Corresponden a los modelos analógicos.
Fuente bibliográfica
“Introducción a la Simulación”. Disponible en < http://wwwdi.ujaen.es/asignaturas/computacionestadistica/pdfs/tema1.pdf>.



















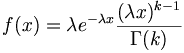
















![1a8e3885d1ec88928dc4e14a6c45000d[1]](https://simulaciondeprocesosempresariales9.files.wordpress.com/2011/02/1a8e3885d1ec88928dc4e14a6c45000d1.png?w=640)
![5df8b002d727f5433eab1c15d5687ff0[1]](https://simulaciondeprocesosempresariales9.files.wordpress.com/2011/02/5df8b002d727f5433eab1c15d5687ff01.png?w=640)